1. Python-for-Probability-Statistics-and-Machine-Learning-2E
  2. chapter
  3. probability
In [1]:
from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
Out[1]:

Worked Examples of Conditional Expectation and Mean Square Error Optimization

Brzezniak [brzezniak1999basic] is a great book because it approaches conditional expectation through a sequence of exercises, which is what we are trying to do here. The main difference is that Brzezniak takes a more abstract measure-theoretic approach to the same problems. Note that you do need to grasp measure theory for advanced areas in probability, but for what we have covered so far, working the same problems in his text using our methods is illuminating. It always helps to have more than one way to solve any problem. I have numbered the examples corresponding to the book and tried to follow its notation.

Example

This is Example 2.1 from Brzezniak. Three coins, 10p, 20p and 50p are tossed. The values of the coins that land heads up are totaled. What is the expected total given that two coins have landed heads up? In this case we have we want to compute $\mathbb{E}(\xi|\eta)$ where

$$ \xi := 10 X_{10} + 20 X_{20} +50 X_{50} $$

where $X_i \in \{0,1\} $ and where $X_{10}$ is the Bernoulli-distributed random variable corresponding to the 10p coin (and so on). Thus, $\xi$ represents the total value of the heads-up coins. The $\eta$ represents the condition that only two of the three coins are heads-up,

$$ \eta := X_{10} X_{20} (1-X_{50})+ (1-X_{10}) X_{20} X_{50}+ X_{10} (1-X_{20}) X_{50} $$

and is a function that is non-zero only when two of the three coins lands heads-up. Each triple term catches each of these three possibilities. For example, the first term equals one when the 10p and 20p are heads up and the 50p is heads down. The the remaining terms are zero.

To compute the conditional expectation, we want to find a function $h$ of $\eta$ that minimizes the mean-squared-error (MSE),

$$ \mbox{MSE}= \sum_{X\in\{0,1\}^3} \frac{1}{2^3} (\xi-h(\eta))^2 $$

where the sum is taken over all possible triples of outcomes for $\{X_{10},X_{20} ,X_{50}\}$ because each of the three coins has a $\frac{1}{2}$ chance of coming up heads.

Now, the question boils down to how can we characterize the function $h(\eta)$? Note that $\eta \mapsto \{0,1\}$ so $h$ takes on only two values. So, the orthogonal inner product condition is the following:

$$ \langle \xi -h(\eta), \eta \rangle = 0 $$

But, because are only interested in $\eta=1$, this simplifies to

$$ \begin{align*} \langle \xi -h(1), 1 \rangle &= 0 \\\ \langle \xi,1 \rangle &=\langle h(1),1 \rangle \end{align*} $$

This doesn't look so hard to evaluate but we have to compute the integral over the set where $\eta=1$. In other words, we need the set of triples $\{X_{10},X_{20},X_{50}\}$ where $\eta=1$. That is, we can compute

$$ \int_{\{\eta=1\}} \xi dX = h(1) \int_{\{\eta=1\}} dX $$

which is what Brzezniak does. Instead, we can define $h(\eta)=\alpha \eta$ and then find $\alpha$. Re-writing the orthogonal condition gives

$$ \begin{align*} \langle \xi -\eta, \alpha\eta \rangle &= 0 \\\ \langle \xi, \eta \rangle &= \alpha \langle \eta,\eta \rangle \\\ \alpha &= \frac{\langle \xi, \eta \rangle}{\langle \eta,\eta \rangle} \end{align*} $$

where

$$ \langle \xi, \eta \rangle =\sum_{X\in\{0,1\}^3} \frac{1}{2^3}(\xi\eta) $$

Note that we can just sweep over all triples $\{X_{10},X_{20},X_{50}\}$ because the definition of $h(\eta)$ zeros out when $\eta=0$ anyway. All we have to do is plug everything in and solve. This tedious job is perfect for Sympy.

In [2]:
import sympy as S
X10,X20,X50 = S.symbols('X10,X20,X50',real=True)
xi  = 10*X10+20*X20+50*X50 
eta = X10*X20*(1-X50)+X10*(1-X20)*(X50)+(1-X10)*X20*(X50)
num=S.summation(xi*eta,(X10,0,1),(X20,0,1),(X50,0,1))
den=S.summation(eta*eta,(X10,0,1),(X20,0,1),(X50,0,1))
alpha=num/den
print(alpha) # alpha=160/3

160/3

This means that

$$ \mathbb{E}(\xi|\eta) = \frac{160}{3} \eta $$

which we can check with a quick simulation

In [3]:
import numpy as np
import pandas as pd
d = pd.DataFrame(columns=['X10','X20','X50'])
d.X10 = np.random.randint(0,2,1000)
d.X10 = np.random.randint(0,2,1000)
d.X20 = np.random.randint(0,2,1000)
d.X50 = np.random.randint(0,2,1000)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-3-77fd94b89e41> in <module>
      1 import pandas as pd
      2 d = pd.DataFrame(columns=['X10','X20','X50'])
----> 3 d.X10 = np.random.randint(0,2,1000)
      4 d.X10 = np.random.randint(0,2,1000)
      5 d.X20 = np.random.randint(0,2,1000)

NameError: name 'np' is not defined

Programming Tip.

The code above creates an empty Pandas data frame with the named columns. The next four lines assigns values to each of the columns. The code above simulates flipping the three coins 1000 times. Each column of the dataframe is either 0 or 1 corresponding to heads-down or heads-up, respectively. The condition is that two of the three coins have landed heads-up. Next, we can group the columns according to their sums. Note that the sum can only be in $\{0,1,2,3\}$ corresponding to 0 heads-up, 1 heads-up, and so on.

In [ ]:
grp=d.groupby(d.eval('X10+X20+X50'))

Programming Tip.

The eval function of the Pandas data frame takes the named columns and evaluates the given formula. At the time of this writing, only simple formulas involving primitive operations are possible.

Next, we can get the 2 group, which corresponds to exactly two coins having landed heads- up, and then evaluate the sum of the values of the coins. Finally, we can take the mean of these sums.

In [ ]:
grp.get_group(2).eval('10*X10+20*X20+50*X50').mean()

The result is close to 160/3=53.33 which supports the analytic result. The following code shows that we can accomplish the same simulation using pure Numpy.

In [ ]:
import numpy as np
from numpy import array
x=np.random.randint(0,2,(3,1000))
print(np.dot(x[:,x.sum(axis=0)==2].T,array([10,20,50])).mean())

In this case, we used the Numpy dot product to compute the value of the heads- up coins. The sum(axis=0)==2 part selects the columns that correspond to two heads-up coins.

Still another way to get at the same problem is to forego the random sampling part and just consider all possibilities exhaustively using the itertools module in Python's standard library.

In [ ]:
import itertools as it
list(it.product((0,1),(0,1),(0,1)))

Note that we need to call list above in order to trigger the iteration in it.product. This is because the itertools module is generator-based so does not actually do the iteration until it is iterated over (by list in this case). This shows all possible triples $(X_{10},X_{20},X_{50})$ where 0 and 1 indicate heads-down and heads-up, respectively. The next step is to filter out the cases that correspond to two heads-up coins.

In [ ]:
list(filter(lambda i:sum(i)==2,it.product((0,1),(0,1),(0,1))))

Next, we need to compute the sum of the coins and combine the prior code.

In [ ]:
list(map(lambda k:10*k[0]+20*k[1]+50*k[2],
         filter(lambda i:sum(i)==2,
         it.product((0,1),(0,1),(0,1)))))

The mean of the output is 53.33, which is yet another way to get the same result. For this example, we demonstrated the full spectrum of approaches made possible using Sympy, Numpy, and Pandas. It is always valuable to have multiple ways of approaching the same problem and cross-checking the result.

Example

This is Example 2.2 from Brzezniak. Three coins, 10p, 20p and 50p are tossed as before. What is the conditional expectation of the total amount shown by the three coins given the total amount shown by the 10p and 20p coins only? For this problem,

$$ \begin{align*} \xi := & 10 X_{10} + 20 X_{20} +50 X_{50} \\\ \eta :=& 30 X_{10} X_{20} + 20 (1-X_{10}) X_{20} + 10 X_{10} (1-X_{20}) \end{align*} $$

which takes on four values $\eta \mapsto \{0,10,20,30\}$ and only considers the 10p and 20p coins. In contrast to the last problem, here we are interested in $h(\eta)$ for all of the values of $\eta$. Naturally, there are only four values for $h(\eta)$ corresponding to each of these four values. Let's first consider $\eta=10$. The orthogonal condition is then

$$ \langle\xi-h(10),10\rangle = 0 $$

The domain for $\eta=10$ is $\{X_{10}=1,X_{20}=0,X_{50}\}$ which we can integrate out of the expectation below,

$$ \begin{align*} \mathbb{E}_{\{X_{10}=1,X_{20}=0,X_{50}\}}(\xi-h(10)) 10 &=0 \\\ \mathbb{E}_{\{X_{50}\}}(10-h(10)+50 X_{50}) &=0 \\\ 10-h(10) + 25 &=0 \end{align*} $$

which gives $h(10)=35$. Repeating the same process for $\eta \in \{20,30\}$ gives $h(20)=45$ and $h(30)=55$, respectively. This is the approach Brzezniak takes. On the other hand, we can just look at affine functions, $h(\eta) = a \eta + b $ and use brute-force calculus.

In [ ]:
from sympy.abc import a,b
h = a*eta + b
eta = X10*X20*30 + X10*(1-X20)*(10)+ (1-X10)*X20*(20)
MSE=S.summation((xi-h)**2*S.Rational(1,8),(X10,0,1),
                (X20,0,1),
                (X50,0,1))
sol=S.solve([S.diff(MSE,a),S.diff(MSE,b)],(a,b))
print(sol)

Programming Tip.

The Rational function from Sympy code expresses a rational number that Sympy is able to manipulate as such. This is different that specifying a fraction like 1/8., which Python would automatically compute as a floating point number (i.e., 0.125). The advantage of using Rational is that Sympy can later produce rational numbers as output, which are sometimes easier to make sense of.

This means that

$$ \begin{equation} \mathbb{E}(\xi|\eta) = 25+\eta \label{_auto1} \tag{1} \end{equation} $$

since $\eta$ takes on only four values, $\{0,10,20,30\}$, we can write this out explicitly as

$$ \begin{equation} \mathbb{E}(\xi|\eta) = \begin{cases} 25 & \text{for}\: \eta=0 \\\ 35 & \text{for}\: \eta=10 \\\ 45 & \text{for}\: \eta=20 \\\ 55 & \text{for}\: \eta=30 \end{cases} \end{equation} \label{eq:ex21sol} \tag{2} $$

Alternatively, we can use orthogonal inner products to write out the following conditions for the postulated affine function:

$$ \begin{equation} \label{eq:ex22a} \tag{3} \langle \xi-h(\eta), \eta \rangle = 0 \end{equation} $$

$$ \begin{equation} \label{eq:ex22b} \tag{4} \langle \xi-h(\eta),1\rangle = 0 \end{equation} $$

Writing these out and solving for $a$ and $b$ is tedious and a perfect job for Sympy. Starting with Equation 3,

In [ ]:
expr=S.expand((xi-h)*eta)
print(expr)

and then because $\mathbb{E}(X_i^2)=1/2=\mathbb{E}(X_i)$, we make the following substitutions

In [ ]:
expr.xreplace({X10**2:0.5, X20**2:0.5,X10:0.5,X20:0.5,X50:0.5})

We can do this for the other orthogonal inner product in Equation 4 as follows,

Programming Tip.

Because Sympy symbols are hashable, they can be used as keys in Python dictionaries as in the xreplace function above.

In [ ]:
S.expand((xi-h)*1).xreplace({X10**2:0.5, 
                             X20**2:0.5,
                             X10:0.5,
                             X20:0.5,
                             X50:0.5})

Then, combining this result with the previous one and solving for a and b gives,

In [ ]:
S.solve([-350.0*a-15.0*b+725.0,-15.0*a-b+40.0])

which again gives us the final solution,

$$ \mathbb{E}(\xi|\eta) = 25+ \eta $$

The following is a quick simulation to demonstrate this. We can build on the Pandas dataframe we used for the last example and create a new column for the sum of the 10p and 20p coins, as shown below.

In [ ]:
d['sm'] = d.eval('X10*10+X20*20')

We can group this by the values of this sum,

In [ ]:
d.groupby('sm').mean()

But we want the expectation of the value of the coins

In [ ]:
d.groupby('sm').mean().eval('10*X10+20*X20+50*X50')

which is very close to our analytical result in Equation 2.

#

Example

This is Example 2.3 paraphrased from Brzezniak. Given $X$ uniformly distributed on $[0,1]$, find $\mathbb{E}(\xi|\eta)$ where

$$ \xi(x) = 2 x^2 $$$$ \eta(x) = \begin{cases} 1 & \mbox{if } x \in [0,1/3] \\\ 2 & \mbox{if } x \in (1/3,2/3) \\\ 0 & \mbox{if } x \in (2/3,1] \end{cases} $$

Note that this problem is different from the previous two because the sets that characterize $\eta$ are intervals instead of discrete points. Nonetheless, we will eventually have three values for $h(\eta)$ because $\eta \mapsto \{0,1,2\}$. For $\eta=1$, we have the orthogonal conditions,

$$ \langle \xi-h(1),1\rangle = 0 $$

which boils down to

$$ \mathbb{E}_{\{x \in [0,1/3]\}}(\xi-h(1))=0 $$$$ \int_0^{\frac{1}{3}}(2 x^2-h(1))dx = 0 $$

and then by solving this for $h(1)$ gives $h(1)=2/24$. This is the way Brzezniak works this problem. Alternatively, we can use $h(\eta) = a + b\eta + c\eta^2$ and brute force calculus.

In [ ]:
x,c,b,a=S.symbols('x,c,b,a')
xi = 2*x**2

eta=S.Piecewise((1,S.And(S.Gt(x,0),
                         S.Lt(x,S.Rational(1,3)))), #  0 < x < 1/3
                (2,S.And(S.Gt(x,S.Rational(1,3)),
                         S.Lt(x,S.Rational(2,3)))), # 1/3 < x < 2/3,
                (0,S.And(S.Gt(x,S.Rational(2,3)),
                         S.Lt(x,1))))               # 1/3 < x < 2/3
h = a + b*eta + c*eta**2 
J=S.integrate((xi-h)**2,(x,0,1))
sol=S.solve([S.diff(J,a), 
             S.diff(J,b),
             S.diff(J,c),
            ],
            (a,b,c))
In [ ]:
print(sol)
print(S.piecewise_fold(h.subs(sol)))

Thus, collecting this result gives:

$$ \mathbb{E}(\xi|\eta) = \frac{38}{27} - \frac{20}{9}\eta + \frac{8}{9} \eta^2 $$

which can be re-written as a piecewise function of x,

$$ \begin{equation} \mathbb{E}(\xi|\eta(x)) =\begin{cases} \frac{2}{27} & \text{for}\: 0 < x < \frac{1}{3} \\\frac{14}{27} & \text{for}\: \frac{1}{3} < x < \frac{2}{3} \\\frac{38}{27} & \text{for}\: \frac{2}{3}<x < 1 \end{cases} \end{equation} \label{eq:ex23a} \tag{5} $$

Alternatively, we can use the orthogonal inner product conditions directly by choosing $h(\eta)=c+\eta b +\eta^2 a$,

$$ \begin{align*} \langle \xi-h(\eta),1\rangle = 0 \\\ \langle \xi-h(\eta),\eta\rangle = 0 \\\ \langle \xi-h(\eta),\eta^2\rangle = 0 \end{align*} \label{eq:ex23b} \tag{6} $$

and then solving for $a$,$b$, and $c$.

In [ ]:
x,a,b,c,eta = S.symbols('x,a,b,c,eta',real=True)
xi  = 2*x**2
eta=S.Piecewise((1,S.And(S.Gt(x,0),
                     S.Lt(x,S.Rational(1,3)))),  #  0 < x < 1/3
            (2,S.And(S.Gt(x,S.Rational(1,3)),
                     S.Lt(x,S.Rational(2,3)))), # 1/3 < x < 2/3,
            (0,S.And(S.Gt(x,S.Rational(2,3)),
                     S.Lt(x,1)))) # 1/3 < x < 2/3
h = c+b*eta+a*eta**2

Then, the orthogonal conditions become,

In [ ]:
S.integrate((xi-h)*1,(x,0,1))
S.integrate((xi-h)*eta,(x,0,1))
S.integrate((xi-h)*eta**2,(x,0,1))

Now, we just combine the three equations and solve for the parameters,

In [ ]:
eqs=[ -5*a/3 - b - c + 2/3,
  -3*a - 5*b/3 - c + 10/27,
  -17*a/3 - 3*b - 5*c/3 + 58/81]
sol=S.solve(eqs)
print(sol)

We can assemble the final result by substituting in the solution,

In [ ]:
print(S.piecewise_fold(h.subs(sol)))

which is the same as our analytic result in Equation 5, just in decimal format.

Programming Tip.

The definition of Sympy's piecewise function is verbose because of the way Python parses inequality statements. As of this writing, this has not been reconciled in Sympy, so we have to use the verbose declaration.

To reinforce our result, let's do a quick simulation using Pandas.

In [ ]:
d = pd.DataFrame(columns=['x','eta','xi'])
d.x = np.random.rand(1000)
d.xi = 2*d.x**2
d.xi.head()

Now, we can use the pd.cut function to group the x values in the following,

In [ ]:
pd.cut(d.x,[0,1/3,2/3,1]).head()

Note that the head() call above is only to limit the printout shown. The categories listed are each of the intervals for eta that we specified using the [0,1/3,2/3,1] list. Now that we know how to use pd.cut, we can just compute the mean on each group as shown below,

In [ ]:
d.groupby(pd.cut(d.x,[0,1/3,2/3,1])).mean()['xi']

which is pretty close to our analytic result in Equation 5. Alternatively, sympy.stats has some limited tools for the same calculation.

In [ ]:
from sympy.stats import E, Uniform
x=Uniform('x',0,1)
E(2*x**2,S.And(x < S.Rational(1,3), x > 0))
E(2*x**2,S.And(x < S.Rational(2,3), x > S.Rational(1,3)))
E(2*x**2,S.And(x < 1, x > S.Rational(2,3)))

which again gives the same result still another way.

Example

This is Example 2.4 from Brzezniak. Find $\mathbb{E}(\xi|\eta)$ for

$$ \xi(x) = 2 x^2 $$

$$ \eta = \begin{cases}2 & \mbox{if } 0 \le x < \frac{1}{2} \\ x & \mbox{if } \frac{1}{2} < x \le 1 \end{cases} \label{eq:ex24} \tag{7} $$

Once again, $X$ is uniformly distributed on the unit interval. Note that $\eta$ is no longer discrete for every domain. For the domain $0 <x < 1/2$, $h(2)$ takes on only one value, say, $h_0$. For this domain, the orthogonal condition becomes,

$$ \mathbb{E}_{\{\eta=2\}}((\xi(x)-h_0)2)=0 $$

which simplifies to,

$$ \begin{align*} \int_0^{1/2} 2 x^2-h_0 dx &= 0 \\\ \int_0^{1/2} 2 x^2 dx &= \int_0^{1/2} h_0 dx \\\ h_0 &= 2 \int_0^{1/2} 2 x^2 dx \\\ h_0 &= \frac{1}{6} \end{align*} $$

For the other domain where $\{\eta=x\}$ in Equation 7, we again use the orthogonal condition,

$$ \begin{align*} \mathbb{E}_{\{\eta=x\}}((\xi(x)-h(x))x)&=0 \\\ \int_{1/2}^1 (2x^2-h(x)) x dx &=0 \\\ h(x) &= 2x^2 \end{align*} $$

Assembling the solution gives,

$$ \mathbb{E}(\xi|\eta(x)) =\begin{cases} \frac{1}{6} & \text{for}\: 0 \le x < \frac{1}{2} \\ 2 x^2 & \text{for}\: \frac{1}{2} < x \le 1 \end{cases} $$

although this result is not explicitly written as a function of $\eta$.

#

Example

This is Exercise 2.6 in Brzezniak. Find $\mathbb{E}(\xi|\eta)$ where

$$ \xi(x) = 2 x^2 $$$$ \eta(x) = 1 - \lvert 2 x-1 \rvert $$

and $X$ is uniformly distributed in the unit interval. We can write this out as a piecewise function in the following,

$$ \eta =\begin{cases} 2 x & \text{for}\: 0 \le x < \frac{1}{2} \\ 2 -2x & \text{for}\: \frac{1}{2} < x \le 1 \end{cases} $$

The discontinuity is at $x=1/2$. Let's start with the $\{\eta=2x\}$ domain.

$$ \begin{align*} \mathbb{E}_{\{\eta=2x\}}((2 x^2-h(2 x)) 2 x)& = 0 \\\ \int_{0}^{1/2} (2x^2-h(2 x) ) 2 x dx &=0 \end{align*} $$

We can make this explicitly a function of $\eta$ by a change of variables ($\eta=2x$) which gives

$$ \int_{0}^{1} (\eta^2/2-h(\eta))\frac{\eta}{2} d\eta =0 $$

Thus, for this domain, $h(\eta)=\eta^2/2$. Note that due to the change of variables, $h(\eta)$ is valid defined over $\eta\in[0,1]$.

For the other domain where $\{\eta=2-2x\}$, we have

$$ \begin{align*} \mathbb{E}_{\{\eta=2-2x\}}((2 x^2-h(2-2x)) (2-2x))& = 0 \\\ \int_{1/2}^{1} (2 x^2-h(2-2x) ) (2-2x) dx &=0 \end{align*} $$

Once again, a change of variables makes the $ \eta$ dependency explicit using $\eta=2-2x$ which gives

$$ \begin{align*} \int_{0}^{1} ((2-\eta)^2/2-h(\eta) ) \frac{\eta}{2} d\eta &=0 \\\ h(\eta) &= (2-\eta)^2/2 \end{align*} $$

Once again, the change of variables means this solution is valid over $\eta\in[0,1]$. Thus, because both pieces are valid over the same domain ($\eta\in[0,1]$), we can just add them to get the final solution,

$$ h(\eta) = \eta^2-2\eta+2 $$

A quick simulation can help bear this out.

In [ ]:
from pandas import DataFrame
import numpy as np
d = DataFrame(columns=['xi','eta','x','h','h1','h2'])
# 100 random samples
d.x = np.random.rand(100)
d.xi = d.eval('2*x**2')
d.eta =1-abs(2*d.x-1)
d.h1=d[(d.x<0.5)].eval('eta**2/2')
d.h2=d[(d.x>=0.5)].eval('(2-eta)**2/2')
d.fillna(0,inplace=True)
d.h = d.h1+d.h2
d.head()

Note that we have to be careful where we apply the individual solutions using the slice (d.x<0.5) index. The fillna part ensures that the default NaN that fills out the empty row-etries is replaced with zero before combining the individual solutions. Otherwise, the NaN values would circulate through the rest of the computation. The following is the essential code that draws Figure.

In [ ]:
%matplotlib inline

from matplotlib.pyplot import subplots
fig,ax=subplots()
ax.plot(d.xi,d.eta,'.',alpha=.3,label='$\eta$')
ax.plot(d.xi,d.h,'k.',label='$h(\eta)$')
ax.legend(loc=0,fontsize=18)
ax.set_xlabel('$2 x^2$',fontsize=18)
ax.set_ylabel('$h(\eta)$',fontsize=18)

Programming Tip.

Basic LaTeX formatting works for the labels in Figure. The loc=0 in the legend function is the code for the best placement for the labels in the legend. The individual labels should be specified when the elements are drawn individually, otherwise they will be hard to separate out later. This is accomplished using the label keyword in the plot commands.

In [ ]:
from matplotlib.pyplot import subplots
from pandas import DataFrame
import numpy as np

d = DataFrame(columns=['xi','eta','x','h','h1','h2'])
# 100 random samples
d.x = np.random.rand(100)
d.xi = d.eval('2*x**2')
d.eta =1-abs(2*d.x-1)
d.h1=d[(d.x<0.5)].eval('eta**2/2')
d.h2=d[(d.x>=0.5)].eval('(2-eta)**2/2')
d.fillna(0,inplace=True)
d.h = d.h1+d.h2

fig,ax=subplots()
_=ax.plot(d.xi,d.eta,'.k',alpha=.3,label=r'$\eta$')
_=ax.plot(d.xi,d.h,'ks',label=r'$h(\eta)$',alpha=.3)
_=ax.set_aspect(1)
_=ax.legend(loc=0,fontsize=18)
_=ax.set_xlabel(r'$\xi=2 x^2$',fontsize=24)
_=ax.set_ylabel(r'$h(\eta),\eta$',fontsize=24)
fig.tight_layout()
fig.savefig('fig-probability/Conditional_expectation_MSE_Ex_005.png')

The diagonal line shows where the conditional expectation equals the $\xi$ function.

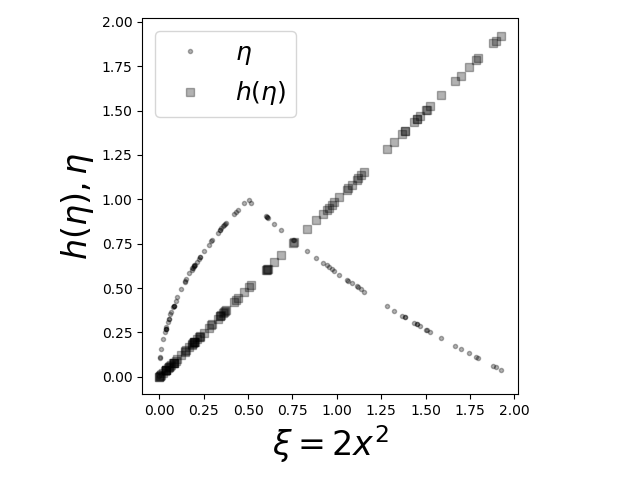
Figure shows the $\xi$ data plotted against $\eta$ and $h(\eta) = \mathbb{E}(\xi|\eta)$. Points on the diagonal are points where $\xi$ and $\mathbb{E}(\xi|\eta)$ match. As shown by the
dots, there is no agreement between the raw $\eta$ data and $\xi$. Thus, one way to think about the conditional expectation is as a functional transform that bends the curve onto the diagonal line. The black dots plot $\xi$ versus $\mathbb{E}(\xi|\eta)$ and the two match everywhere along the diagonal line. This is to be expected because the conditional expectation is the MSE best estimate for $\xi$ among all functions of $\eta$.

Example

This is Exercise 2.14 from Brzezniak. Find $\mathbb{E}(\xi|\eta)$ where

$$ \xi(x) = 2 x^2 $$$$ \eta = \begin{cases} 2x & \mbox{if } 0 \le x < \frac{1}{2} \\ 2x-1 & \mbox{if } \frac{1}{2} < x \le 1 \end{cases} $$

and $X$ is uniformly distributed in the unit interval. This is the same as the last example and the only difference here is that $\eta$ is not continuous at $x=\frac{1}{2}$, as before. The first part is exactly the same as the first part of the prior example so we will skip it here. The second part follows the same reasoning as the last example, so we will just write the answer for the $\{\eta = 2x-1\}$ case as the following

$$ h(\eta)=\frac{(1+\eta)^2}{2} , \: \forall \eta \: \in [0,1] $$

and then adding these up as before gives the full solution:

$$ h(\eta)= \frac{1}{2} +\eta + \eta^2 $$

The interesting part about this example is shown in Figure. The dots show where $\eta$ is discontinuous and yet the $h(\eta)=\mathbb{E}(\xi|\eta)$ solution is equal to $\xi$ (i.e., matches the diagonal). This illustrates the power of the orthogonal inner product technique, which does not need continuity or complex set-theoretic arguments to calculate solutions. By contrast, I urge you to consider Brzezniak's solution to this problem which requires such methods.

In [ ]:
d = DataFrame(columns=['xi','eta','x','h','h1','h2'])
d.x = np.random.rand(100) # 100 random samples
d.xi = d.eval('2*x**2')
d['eta']=(d.x<0.5)*(2*d.x)+(d.x>=0.5)*(2*d.x-1)
d.h1=d[(d.x<0.5)].eval('eta**2/2')
d.h2=d[(d.x>=0.5)].eval('(1+eta)**2/2')
d.fillna(0,inplace=True)
d.h = d.h1+d.h2
fig,ax=subplots()
_=ax.plot(d.xi,d.eta,'.k',alpha=.3,label='$\eta$')
_=ax.plot(d.xi,d.h,'ks',label='$h(\eta)$',alpha=0.3)
_=ax.set_aspect(1)
_=ax.legend(loc=0,fontsize=18)
_=ax.set_xlabel('$2 x^2$',fontsize=24)
_=ax.set_ylabel('$h(\eta),\eta$',fontsize=24)
fig.tight_layout()
fig.savefig('fig-probability/Conditional_expectation_MSE_Ex_006.png')

The diagonal line shows where the conditional expectation equals the $\xi$ function.

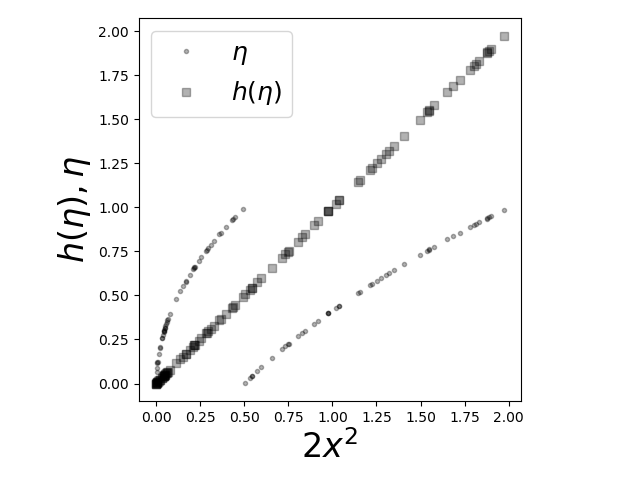
Extending projection methods to random variables provides multiple ways for calculating solutions to conditional expectation problems. In this section, we also worked out corresponding simulations using a variety of Python modules. It is always advisable to have more than one technique at hand to cross-check potential solutions. We worked out some of the examples in Brzezniak's book using our methods as a way to show multiple ways to solve the same problem. Comparing Brzezniak's measure-theoretic methods to our less abstract techniques is a great way to get a handle on both concepts, which are important for advanced study in stochastic process.